nLab group object
Context
Categorical algebra
internalization and categorical algebra
-
algebra object (associative, Lie, …)
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Contents
Idea
A group object in a cartesian category is a group internal to (see at internalization for more on the general idea).
In other words, a group object is something that behaves “just like” a group but which need not have (just) an underlying set.
For example, group objects in Top are topological groups, while group objects in SmthMfd are Lie groups, etc., see the Examples below.
Given a non-cartesian but braided monoidal category one can still make sense of group objects in the dual guise of Hopf monoids, see there for more and see further below.
Definition
In a cartesian monoidal category
Definition
(group object in cartesian monoidal category)
A group object or internal group internal to a category with finite products (binary Cartesian products and a terminal object ) is
-
an object in (say with the unique morphism to the terminal object)
-
and morphisms in as follows:
such that the following diagrams commute:
Remark
More pedantically, the associativity law (1) actually factors through the associator isomorphisms , which is notationally suppressed above.
Remark
The pairing denotes where is a diagonal morphism.
Remark
Even if does not have all binary products, as long as products with (and the terminal object ) exist, then one can clearly still speak of a group object in , as above.
Remark
The first two structures in Def. (binary operation and neutral element) together with the first two properties (associativity and unitality) make a internal monoid object. The remaining structure (inverses) is what specializes this monoid object to a group object.
There is an alternative way to encode the specialization from monoid objects to group objects:
Proposition
A monoid object can be made into a group object according to Def. iff its associativity diagram (1) is cartesian (meaning: exhibiting a pullback or fiber product).
Proof
First assume that becomes a group object via some . In order to show that then (1) is Cartesian we may verify the universal property of a fiber product:
Given any domain and morphisms
such that the following solid diagram commutes
we need to show that there exists a unique dashed morphism making the left and right triangles commute.
By alternative projection to the two factors in the codomain of these triangles, one immediately finds that the dashed morphism must be equal to both
which is indeed consistent by the assumption that the solid diagram commutes, and using again the assumed inverses, since this says that:
Conversely, assuming that the associativity square is Cartesian, we need to produce a consistent inverse-assigning map. To this end, specialize the maps in (4) to and
whence the dashed map (5) gives
from which we may project out the desired map , that one readily checks to satisfy the invertibility law.
In a braided monoidal category
Notice (with Rem. ) that the use of diagonal maps in Def. precludes direct generalization of this definition of group objects to non-cartesian monoidal categories, where such maps in general do not exist.
Hence, while the underlying monoid object may generally be defined in any monoidal category, the internal formulation of existence of inverse elements typically uses extra structure, such as that of a compatible comonoid object-structure to substitute for the missing diagonal maps.
Given this, inverses may be encoded by an antipode map and the resulting “monoidal group objects” are known as Hopf monoids. These subsume and generalize Hopf algebras, which are widely studied, for instance in their role as quantum groups.
Hopf monoids may be defined in any symmetric monoidal category, or more generally any braided monoidal category, where the braiding is used in stating the fact that the comultiplication is a homomorphism of monoid objects.
In terms of presheaves of groups
Proposition
Given a cartesian monoidal category , the category of internal groups in (in the sense of Def. ) is equivalent to the full subcategory of the category of presheaves of groups on , spanned by those presheaves whose underlying set part in is representable.
This is a special case of the general theory of structures in presheaf toposes.
It means that the forgetful functor from the functor category to the presheaf category (obtained by composing with the forgetful functor Grp Set) creates representable group objects from representable objects.
We unwind how this works:
An object in equipped with internal group structure is identified equivalently with a diagram of functors of the form
where is the opposite category of , Grp is the category of groups with group homomorphisms between them, and Set is the category of sets with maps/functions between them. Finally,
is the Yoneda embedding of into its category of presheaves , which sends each object to the representable presheaf that it represents.
Since the Yoneda embedding is fully faithful, it is natural to leave it notationally implicit and to write (for ) as shorthand for
(This a also referred to as “ seen at stage ”, or similar.)
Now, the lift (6) of such a presheaf of sets to a presheaf of groups equips for each object the set with an ordinary group structure , in particular with a product operation (a map of sets) of the form
Moreover, since morphisms in Grp are group homomorphisms, it follows that for every morphism in we get a commuting diagram of the form
Taken together this means that there is a morphism
of representable presheaves. By the Yoneda lemma, this uniquely comes from a morphism in , which is the product of the group structure on the object that we are after.
etc.
As data structure
In the language of dependent type theory (using the notation for dependent pair types here) the type of group data structures is:
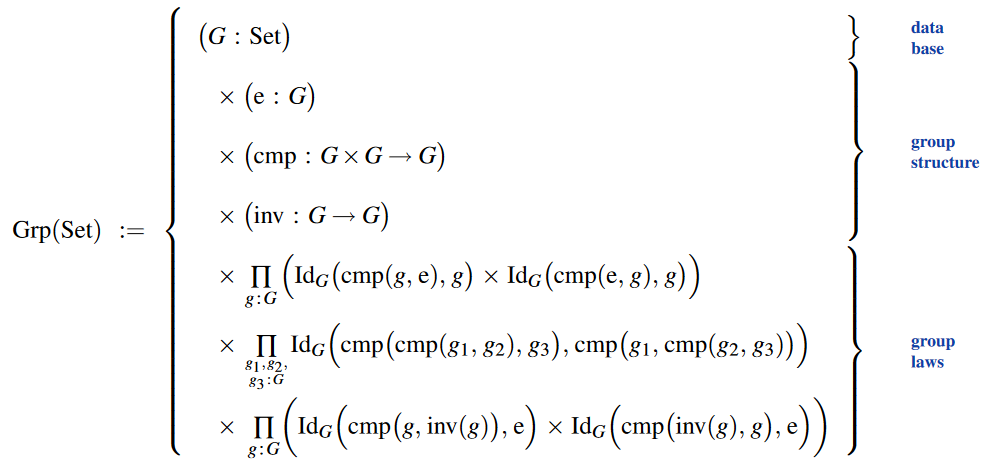
Examples
-
A group object in TopologicalSpaces is a topological group.
-
A group object in SimplicialSets is a simplicial group.
-
A group object in SDiff is a super Lie group.
-
A group object in Grp is an abelian group (using the Eckmann-Hilton argument).
-
A group object in Ab is an abelian group again.
-
A group object in Grpd is a strict -group again.
-
A group object in CRing is a commutative Hopf algebra.
-
A group object in a functor category is a group functor.
-
A group object in schemes is a group scheme.
-
A group object in an opposite category is a cogroup object.
-
A group object in G-sets/G-spaces is a -equivariant group, namely a semidirect product group.
-
A group object in stacks is a group stack.
Theory
The basic results of elementary group theory apply to group objects in any category with finite products. (Arguably, it is precisely the elementary results that apply in any such category.)
The theory of group objects is an example of a Lawvere theory.
Related concepts
-
group, group object, group object in an (∞,1)-category
-
groupoid, groupoid object, groupoid object in an (∞,1)-category
-
infinity-groupoid, infinity-groupoid object, groupoid object in an (∞,1)-category
References
The general definition of internal groups seems to have first been formulated in:
- Alexander Grothendieck, p. 104 (7 of 21) of: FGA Techniques de construction et théorèmes d’existence en géométrie algébrique III: préschémas quotients, Séminaire Bourbaki: années 1960/61, exposés 205-222, Séminaire Bourbaki, no. 6 (1961), Exposé no. 212, (numdam:SB_1960-1961__6__99_0, pdf, English translation: web version)
following the general principle of internalization formulated in:
- Alexander Grothendieck, p. 340 (3 of 23) in: FGA Technique de descente et théorèmes d’existence en géométrie algébriques. II: Le théorème d’existence en théorie formelle des modules, Séminaire Bourbaki : années 1958/59 - 1959/60, exposés 169-204, Séminaire Bourbaki, no. 5 (1960), Exposé no. 195 (numdam:SB_1958-1960__5__369_0, pdf, English translation: web version)
reviewed in:
- Barbara Fantechi, Lothar Göttsche, Luc Illusie, Steven L. Kleiman, Nitin Nitsure, Angelo Vistoli, Section 2.2 of: Fundamental algebraic geometry. Grothendieck’s FGA explained, Mathematical Surveys and Monographs 123, Amer. Math. Soc. (2005) [MR2007f:14001, ISBN:978-0-8218-4245-4, lecture notes]
On internalization, H-spaces, monoid objects, group objects in algebraic topology/homotopy theory and introducing the Eckmann-Hilton argument:
-
Beno Eckmann, Peter Hilton, Structure maps in group theory, Fundamenta Mathematicae 50 (1961), 207-221 (doi:10.4064/fm-50-2-207-221)
-
Beno Eckmann, Peter Hilton, Group-like structures in general categories I multiplications and comultiplications, Math. Ann. 145, 227–255 (1962) (doi:10.1007/BF01451367)
-
Beno Eckmann, Peter Hilton, Group-like structures in general categories III primitive categories, Math. Ann. 150 165–187 (1963) (doi:10.1007/BF01470843)
With emphasis of the role of the Yoneda lemma:
- Saunders MacLane, chapter III, section 6 in: Categories for the Working Mathematician, Springer (1971)
Review:
-
John Michael Boardman, Algebraic objects in categories, Chapter 7 of: Stable Operations in Generalized Cohomology [pdf, pdf] in: Ioan Mackenzie James (ed.) Handbook of Algebraic Topology Oxford (1995) [doi:10.1016/B978-0-444-81779-2.X5000-7]
-
Magnus Forrester-Barker, Group Objects and Internal Categories [arXiv:math/0212065]
In the broader context of internalization via sketches:
- Michael Barr, Charles Wells, Section 4.1 of: Toposes, Triples, and Theories, Originally published by: Springer-Verlag, New York, 1985, republished in: Reprints in Theory and Applications of Categories, No. 12 (2005) pp. 1-287
With focus on internalization in sheaf toposes:
- Saunders Mac Lane, Ieke Moerdijk, Section II.7 of: Sheaves in Geometry and Logic, Springer 1992 (doi:10.1007/978-1-4612-0927-0)
Last revised on December 11, 2024 at 17:52:16. See the history of this page for a list of all contributions to it.